|
Основные положения
Показано, что в гравитационном поле планеты, при вращении уравновешенной системы материальных точек, под действием центробежных сил инерции возникает компонента, направленная вдоль оси вращения системы, т.е. масса, притягивается к Земле не по вертикали, а с учетом кривизны гравитационного поля, под некоторым углом к ней.
Сделан вывод (посредством суперпозиции векторов), что 100% потеря веса вращающегося кольца, не зависимо от радиуса и массы, происходит при линейной скорости вращения:
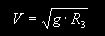
где g = 9,81 м/с2, R3 = 6371 км.
Для вывода уравнения антигравитационной силы рассмотрим уравновешенную систему материальных точек, вращающихся вокруг неподвижной оси (импровизированный гироскоп): разнос грузиков или тонкое кольцо массой mk Ось системы направлена вертикально поверхности Земли, направление которой проходит через центр Земли (рис.1). Вес центра вращающейся системы в расчете учитывать не будем.
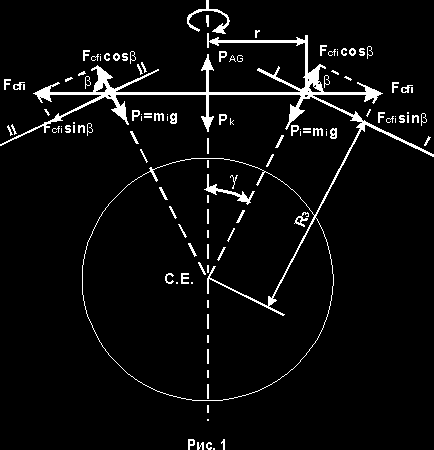
Так как мы рассматриваем взаимодействие вращающегося тела с Землей, принципиальное значение имеет истинное, т.е. фактическое направление векторов действующих на материальную точку сил, и соответственно, вектор силы тяжести Pi материальных точек будет образовывать угол bк оси вращения системы (рис.1).
Для наглядности на рисунке изображен несоизмеримо большой радиус r вращающейся системы относительно Земли, радиус которой R3. Расставим векторы действующих на материальную точку сил, и для наглядности, изобразим нормальные плоскости I-I и II-II, где силы веса материальных точек являются перпендикулярами.
Обратим внимание на парадокс, когда уравновешенные, центробежные силы инерции одной вращающейся системы вследствие кривизны гравитационного поля фактически направлены от Земли.
Для вывода уравнения имеем:
Pi = mig - сила тяжести материальной точки.
Fcfi = miV2/r - центробежная сила инерции материальной точки.
Fcficos(b) - составляющая Fcfi на угол b, так как фактически таковой имеется.
Составляющая Fcfisin(b) на расчет влияния не оказывает, т.к. действует перпендикулярно силе тяжести и потому в расчете не учитывается.
Для того чтобы каждая материальная точка системы находилась в невесомости, должно удовлетворяться соотношение:
mig - Fcficos(b) = 0, где
Fcficos(b) = miV2cos(b)/r
V - окружная скорость вращения системы
cos(b) = sin(g) = r/R3 , если вращение происходит близко к поверхности Земли.
Подставим значения
Fcficos(b) = (miV2/r)(r/R3) = miV2/R3
Если окружная скорость V = VI и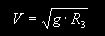 что является первой космической скоростью, получим: что является первой космической скоростью, получим:
Fcficos(b) = miV2/R3 = migR3/R3 = mig, соответственно имеем:
mig - mig = 0, что является условием невесомости.
В целом на кольцо будут действовать силы:
Pk - сила тяжести кольца, приложенная в центре масс, равная для кольца
Pk = ∑mig = mg, направленная вниз, к Земле,
и сила, направленная противоположно силе Pk, приложенная в центре масс, назовем ее "антигравитационная" и обозначим PAG, которая равна:
PAG = mV2/R3, при скорости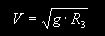
PAG = mg, направленная вверх, от Земли.
Отметим парадокс: на неподвижный центр системы действуют и определяются силы, равно, как и на движущееся над поверхностью Земли тело.
Силу PAG иначе, как "антигравитацмонная" назвать невозможно, так как она отвечает признакам:
- противоположно направлена силе тяготения (гравитационной силе);
- неконтактна, не являясь электромагнитной.
Этот вывод многократно экспериментально подтвержден энтузиастами, которые в поисках антигравитационной силы исследуют гироскоп и при том совершенно справедливо заявляют о снижении веса.
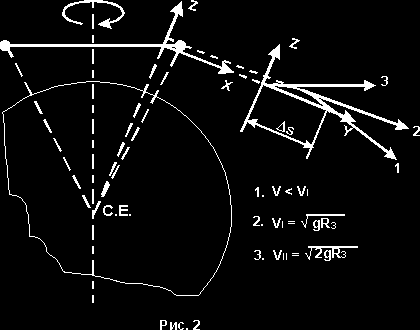
Если отсечь дугу DS (рис.2) то, глядя на проекцию движения материальных точек можно прогнозировать направление векторов скорости при различных окружных скоростях всей системы.
Примеры расчетов
Исходные данные:
R3 = 6371км
mk = 100кг
g = 9,81м/с2
V0 = 5000м/c
VI = (gR3)1/2
VII = (2gR3)1/2
Определим PAG
V0 = 5000 м/c , PAG = mkV2/R3 = 392,4 Н
В данном случае кольцо, вращаясь будет опускаться на Землю под действием силы:
P = Pk - PAG = 588,6 H
с ускорением g0 = 5,89 м/c2.
VI = (gR3)1/2,
PAG = mkV2/R3 = mkg = 981 H
Кольцо будет в состоянии невесомости, так как
Pk = PAG.
VII = (2gR3)1/2,
PAG = mkV2/R3 = 2mkg = 1962 H
Кольцо будет подниматься вверх под действием
силы PAG - Pk = 981 H с ускорением 1 g.
Летательный аппарат
Очень хотелось бы на основании вышеизложенного вывода спроектировать летательный аппарат (ЛА), но как видно из расчета при достижении требуемой скорости на окружности возникнут мегатонные центробежные силы инерции, а в настоящее время удержать их нечем. Но пофантазировать на эту тему можно, тем более, при вращении кольца над поверхностью Земли может возникать интересное свойство.
Заключим в прочный и легкий корпус 1 (рис. 3) два диска 2 расположенных на одной оси, с массой распределенной по окружности. Откачаем из корпуса воздух и в вакууме раскрутим двигателем 3 диски в противоположные направления (создадим механический диполь) для исключения реактивного момента на корпус ЛА. При скорости на окружности дисков V > VI, когда антигравитационная сила PAG превзойдет силу тяжести дисков и корпуса ЛА, аппарат взлетит. Но с такой простой схемой взлет ЛА будет не вертикальным, так как на аппарат с первых секунд полета будет действовать гироскопический момент и аппарат получит перекос.
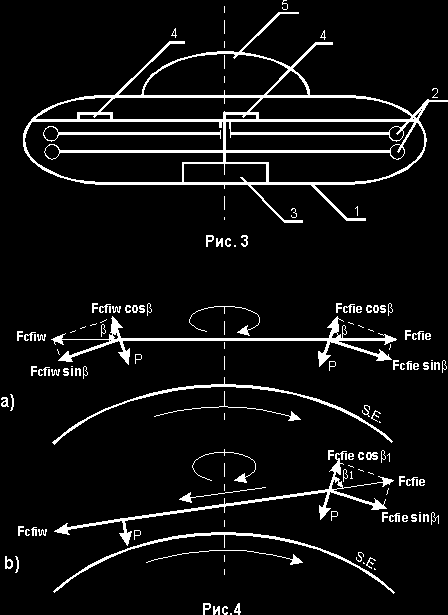
На рис. 4 изображены силы, действующие на вращающийся диск в уравновешенном состоянии и при перекосе. При перекосе, сила действующая против вращения Земли Fcfiwsin(b) = Fcfiw , будет на величину Fcfiecos(b1) больше противодействующей ей силы Fcfiesin(b1), действующей по вращению Земли (нижний индекс "w" и "e" обозначают соответственно западную и восточную стороны). ЛА, под действием разности сил, будет двигаться против вращения Земли (на запад) (свойство вертолетного винта) ускоренно, пока не зафиксируется в пространстве относительно Звездного Свода. Можно считать, что не аппарат будет лететь над Землей, а Земля будет вращаться под аппаратом.
Вероятно, данным процессом можно будет управлять, например, при помощи груза 4, который можно перемещать в требуемую сторону. Для управления летательным аппаратом предусмотрена кабина 5, в которой может разместиться экипаж и необходимый полезный груз.
Заключение
Некоторые ученые, изыскивая подвох в этом простейшем выводе, считают, что центробежная сила инерции, внутренняя, а потому внешнего воздействия оказывать, не может.
С тем, что центробежная сила инерции является внешней, специалисты в области теоретической механики согласились давно, вот одна из цитат:
"В неинерциальных системах отсчета (та, что рассматривалась выше) наряду с "обычными" силами действуют силы инерции. Эти силы всегда являются внешними по отношению к рассматриваемым телам. Следовательно, в этих системах не существует, замкнутых систем материальных тел и поэтому нет законов сохранения энергии, импульса и момента импульса в обычном смысле
(А. Н. Матвеев "Механика и теория относительности" 1986 г. стр. 168)".
Для того чтобы убедиться в том, что центробежная сила инерции внешняя, достаточно подержать гироскоп в руках. Те, кто держал гироскоп в руках, знают, что его, как футбольный мяч по земле не покатишь. Для того чтобы вывести гироскоп из плоскости вращения, т.е. приодалеть центробежную силу инерции, надо приложить именно внешнюю силу.
В выше упомянутом учебнике А. Н. Матвеева "Механика и теория относительности" в начале раздела "Законы сохранения" автор приводит высказывание, которое как бы определяет верхнюю границу всей науки механики:
"Например, пусть нас интересует движение тела, но мы не в состоянии решить уравнение этого движения, и по этому не знаем не только, где это тело будет в тот или иной момент времени, но и будет ли оно при своем движении находиться вблизи поверхности Земли или покинет Землю, отправившись в межпланетное путешествие. Если при этих условиях нам удастся, не имея решения уравнений, установить, что тело будет двигаться вблизи Земли, и предсказать, что ни при каких условиях оно не удалится от поверхности Земли дальше, например, чем на 10 км, то это будет существенным успехом. А если еще удастся установить, что на высоте 10 км скорость тела будет равна нулю, и указать, какое направление должна иметь заданная скорость на Земле, чтобы оно достигло высоты 10 км, то, в сущности, для определенных целей нам известно все об этом движении и вообще нет необходимости решать уравнения".
Я согласен с автором этих строк и к новым поискам в механике отношусь с пессимизмом
|



