Неинерциальные замкнутые системы
и обоснование безопорного движения

Иванов Андрей Алексеевич
г.Магадан

Уважаемые господа, как гласит закон сохранения импульса в замкнутой системе - "Если сумма внешних сил равна нулю, то импульс системы сохраняется". Это закон, причем закон природы, а как известно, законы мироздания не изобретают, их выводят на основании опытов и расчетов из уже существующих законов и формул. Однако, даже законы природы "выводят" люди, и, как известно, они иногда ошибаются.

Чтобы Вы могли оценить вышеприведённую трактовку закона сохранения импульса, предлагаю мысленно представить следующую ситуацию: Вы находитесь на неподвижно висящем в пространстве космическом корабле, и перед вами находиться маховик в статичном состоянии. Станина, на которой он расположен, пристегнута к полу зажимами, и по её бокам предусмотрены ручки, за которые вы вполне можете поднять маховик от пола.

Теперь представьте, что вы раскрутили маховик. Соответственно этим вы передадите кораблю определенный импульс - так, кстати, работают системы центровки космических кораблей. А теперь представьте, что, раскрутив маховик, вы отстегнули его от пола и подняли. Как известно, маховик не имеет направленного вектора силы, так что вы вполне можете его подержать, или спокойно развернуть на 90 градусов. При этом, никакого влияния на вращение корабля ваши действия не окажут. А теперь представьте, что, развернув маховик на 90 градусов, вы снова пристегнули его к полу и остановили, тем самым, передав заранее накопленный импульс обратно кораблю.

Останется ли суммарный импульс корабля неизменным после приложения к нему двух перпендикулярно направленных импульсов? Формально - да. Общеизвестно, что суммарный импульс вращения равен нулю. Но в момент раскручивания и остановки маховика на предметы внутри корабля будут действовать силы не характерные для инерциальных систем. А ведь космический корабль - замкнутая инерциальная система. Или нет? Но если нет, значит, она неинерциальная, соответственно мы можем использовать этот факт для получения дополнительного импульса?

Ответ на вопрос довольно прост, но чтобы вам было проще его понять, я приведу более легкий, и очевидный пример - скажите, можно ли поместить кубик льда в аналогичную ему по форме ёмкость, но с узким горлышком? И да, и нет. Нет, потому что он не пройдет в узкое горлышко. Да, потому что, растопив лед, мы можем влить воду в ёмкость и заморозить её. Так и в вопросе о замкнутых системах - совокупность векторов импульсов в них всегда будет равна, но! Использование маховика как накопителя безвекторной кинетической энергии, вкупе с неинерциальными свойствами перехода потенциальной энергии в кинетическую, дает очень интересные результаты. Какие? На этот вопрос я и постараюсь ответить в этой статье, заодно рассказав, о уже существующем доказательстве неинерционности данных систем - безопорном двигателе.

Как известно линейный безопорный двигатель создать невозможно. Нельзя получить прямолинейное движение, не передав при этом "точке опоры" равного, а главное обратного по направлению количества кинетической энергии. И я не собираюсь оспаривать этот очевидный факт, но… безопорный двигатель все же существует, более того, не на бумаге, а в действующей модели, прошедшей "безопорные" испытание на крутильных весах.

И это не ошибка господа, и тем более не чудо. Это всего лишь использование элементарных законов физики. Просто сотни моих предшественников, польстившись на наиболее очевидное с первого взгляда решение, не только обрекли себя на заведомую неудачу, но и создали дурную славу данному направлению исследований.

Итак, мы знаем, что "оттолкнуться" от гипотетической "точки опоры" всё же возможно, но получить желаемое ускорение нельзя, так как сумма векторов процесса "торможения" будет равна первоначальному импульсу ускорения. Однако, поступательное движение не единственная форма существования кинетической энергии, поэтому давайте обратимся к иной её форме - вращению. Тем более, что "точкой опоры" в этом случае будет маховик - поистине идеальная "точка опоры". Во-первых, вращающийся маховик не имеет направленного вектора силы, во вторых, он способен сохранять накопленную энергию необходимое нам время.

А далее, чтобы сразу расставить все точки над "i", проведём довольно простой эксперимент: возьмем штангу, с одного конца которой будет расположен электродвигатель с маховиком, с другой, противовес. Затем подвесим данную конструкцию на нити, закреплённой в точке соответствующей центру тяжести испытуемого прибора. При этом, штанга должна располагаться параллельно пола а ось вращения электродвигателя перпендикулярно пола.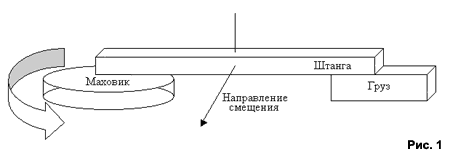

Теперь, включив двигатель на короткое время, мы получим следующий результат - в тот момент, когда маховик начинает раскручиваться влево, штанга с противовесом начинает круговое движение вправо. При этом общий центр тяжести заметно смешается по ходу вращения! Позже, по мере остановки маховика, вращение штанги с противовесом почти прекращается, изменяя направление вращения. При этом конструкция не замирает на месте, а продолжает раскачиваться на нити.

Обсуждение применения закона сохранения импульса в данной системе мы можем оставить на потом, т.к. схожий процесс будет рассмотрен несколько позже, но уже в замкнутой системе. В данном случае нам важен сам факт смещения общего центра тяжести относительно точки покоя.

Итак, опыт наглядно показывает, что смещение общего центра тяжести конструкции маховик, штанга, противовес - возможно. А раз смещение общего центра масс возможно, то мы вполне можем использовать данный факт для получения импульса движения.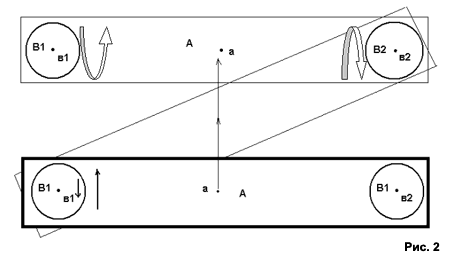

Начнем с того, что определим составляющие системы. А - штанга, В1 и В2 идентичные маховики (они же эл. двигатели в реальном двигателе). При этом, для удобства вычисления импульса движения, отметим центры масс деталей А, В1 и В2 как совокупность материальных точек составляющих данные объекты, соответственно А-а, В1-в1 и В2-в2.

Теперь рассмотрим поведение системы в первой фазе движения - взаимодействие маховика В1 с АВ2.

Приложив силу F для вращения маховика мы получим взаимное противоположное вращение АВ2 - В1 вокруг точки в1 т.к. она является совокупным центром векторов силы воздействующих по окружности маховика (о влиянии центробежной силы действующей относительно АВ1В2 чуть позже).

Согласно третьему закону Ньютона F_А+F_В2 = -F_В1.

При этом следует учесть и тот факт, что согласно тому же третьему закону Ньютона, F_А = F_В2.

Учитывая, что исходная наша задача определить общее направление движения АВ1В2, определим тот импульс р для каждой из частей конструкции, что придаст им использование силы взаимодействия F относительно взаимодействия АВ2 - с маховиком В1.

Но так как все три тела состоят по определению из абсолютно упругой среды, перемещение любого из них в пространстве будет соответствовать совокупности перемещения материальных точек, из которых эти тела состоят. Соответственно, корректным будет использование ранее отмеченных точек а, в1, в2, так как:

А) именно они будут отражать общее поступательное движение всей совокупности материальных точек каждого из объектов исследования.

Б) именно на них не будут действовать центростремительные силы того объекта, тенденцию передвижения которого они отражают.

В) их расстояние всегда будет неизменным, так как В1 и В2 соответствуют осям соединения АВ1 и АВ2.

Теперь нам необходимо вычислить какой импульс придаст воздействие силы F на каждую составную системы.

При исчислении направления движения налицо классический пример применения формулы момента силы М.

Для В1 момент силы М имеет отрицательное значение (по часовой стрелке), для А и В2 - положительное.

При этом вершиной угла для всех точек является точка в1 как ось вращения (именно в ней сходится совокупный вектор силы приложенной по окружности В1).

Как видно из рис.2 "плечом силы" для совокупности всех материальных точек всей системы АВ1В2 является точка а (как общий центр трех взаимосвязанных частей).

Соответственно:

М_а = F_А(а-в1), где а-в1 = 1/2, М_а = F_А/2
М_в2 = F_В2(а-в2), где а-в1 = 1, М_в2 = F_В2
М_в1 = F_В1(в1-в1), где в1-в1 = 0, М_в1 = 0
М_АВ1В2 = F (а-в1), где а-в1 = 1/2, М_АВ1В2 = F/2

При этом, необходимо учитывать, что взаимодействие частей АВ1 все же придаст В1 некий импульс силы, но он будет существенно меньше совокупности импульсов АВ2.

Соответственно М_А+М_В2 <> -М_В1 - что вполне подтверждает как вполне очевидный факт вращения системы АВ1В2, так и куда более интересный для нас факт наличия положительного p и М_А у всей системы М_АВ1В2.

Учитывая распределение приложенной к системе силы F_А+F_В2 = -F_В1.

Мы без труда можем выяснить что:

М_а = F_А/2
где F_А+F_В2 = -F_В1
при F_А = F_В2
F_А = F/2

Соответственно p_А = М_А = F что соответствует и общему поступательному импульсу системы, так как материальная точка а соответствует общему центру тяжести АВ1В2.

Соответственно полезная работа данной фазы движения:

А = Fa/4
Где a - угол поворота АВ2.

А из соотношения М_АВ1В2= F/2 - М_А = F/4 = М_АВ1В2= F/4 мы видим и ту часть импульса, которая составит вращение системы.

При этом необходимо особо отметить тот факт, что приведенные выше расчеты характерны лишь при секторном смещении частей АВ2 и полном вращении В1, с трансформацией движения по окружности в движение по синусоиде. Взаимное же вращение АВ2 - В1, как и расчеты с использованием абсолютных величин вращения, лишь исказят реально происходящий процесс.

Однако, это не относиться к целенаправленному равномерному вращению АВ2-В1, с использованием секторов ускорения - торможения.

В данном случае - движение по окружности, это движение по замкнутой прямой, которую мы можем разорвать и получить пусть несколько изогнутую, но дорогу к звездам.

Теперь, когда мы определили распределение импульсов системы, пора обратить внимание иные составляющие процесса движения.

Итак, налицо явное нарушение закона сохранения импульса в замкнутой системе?

Проще говоря р_АВ2 <> р_В1. Где р - импульс материальной точки.

Конечно, данное неравенство корректно только к совокупности материальных точек каждого из объектов исследования. Импульс любой отдельно взятой материальной точки (исключая в1) будет больше нуля, и формулу М_А+М_В2 <> -М_В1 можно будет рассматривать как производную кинетической энергии, но… нас то интересует как раз совокупность движения.

И действительно, факт отсутствия направленного импульса р во вращающемся вокруг центра тяжести однородном твёрдом теле общеизвестен.

Такие же экспериментальные данные даёт и опыт приведённый в начале данного исследования.

При этом ссылка на возможное круговое движение системы АВ1В2 без дополнительного поступательного движения уже в момент самого импульса, не имеет под собой ни практического (см. опыт на рис.1) ни теоретического обоснования, так как центробежные и центростремительные силы, уравняют вращение АВ1В2 вокруг общего центра тяжести только после полного оборота системы.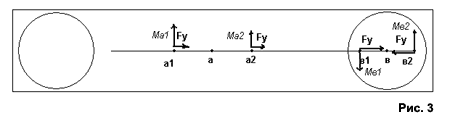

Именно в работе центростремительных и центробежных сил кроется ответ на столь несвойственное "закону сохранения импульса" поведение системы АВ1В2.

Но будем последовательны, и чтобы понять процессы происходящие во время взаимодействия деталей АВ2 - В1 рассмотрим воздействие совокупности сил на четыре материальные точки. Две из них разместим на равном удалении от общего центра масс и обозначим как а1 и а2. Две разместим на маховике В1 (так же равноудалено от центра тяжести маховика) и обозначим как в1 и в2.

Как следует из вышесказанного, во время приложения силы между конструкцией АВ2 и маховиком В1 на каждую из материальных точек системы будет действовать момент силы М = -Fd, где расстояние между данной точкой и центром вращения в. Учитывая что для всех выбранных точек d <> 0 мы можем утверждать что:

1. Импульс каждой материальной точки будет больше 0.

2. Согласно третьему закону Ньютона - F_а1+F_а2=F_в1+F_в2

Однако, материальные точки в1 и в2 диаметрально противоположны относительно общего центра вращения - соответственно сила упругости - F_упр (или центростремительная сила) компенсирует возникшую центробежную силу независимо от скорости их движения.

Материальные же точки а1 и а2 находятся на одной прямой относительно общего центра вращения в, их совокупный импульс будет больше 0, и направлен в одном направлении.

Они не будут двигаться прямолинейно, это видно из рис. 3, 4, и на них так же будет действовать центростремительная сила. Однако, обусловленная соотношением масс "до" оси вращения и "за" ней, она будет меньше центробежной силы.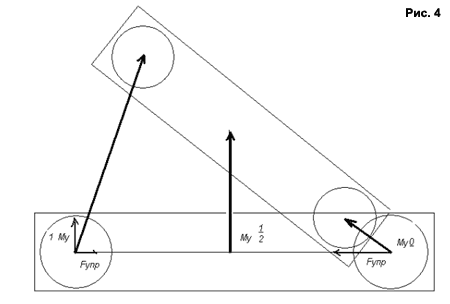

При этом следует отметить еще один факт. Как только взаимодействие между маховиком и остальной системой прекратиться, все материальные точки системы АВ1В2 продолжат свое движение согласно полученному импульсу силы.

При этом, скорость материальной точки соответствующей оси вращения АВ2 - В1 будет согласно полученному моменту силы М= Fd, где d=0 равна 0. В то же время скорость противоположной ей относительно центра массы а материальной точки соответствующей оси соединения АВ2 - М=Fd, где d будет иметь максимально большое значение для всей конструкции, и соответственно не будет равно 0.

Но так как конструкция по определению состоит из абсолютно упругой среды, то расстояние между любыми материальными точками детали А не может увеличиться за счет разности их скоростей. Соответственно в действие вступит сила упругости, обуславливающая центростремительную силу, и наличие дополнительного вектора для каждой материальной точки (исключая абсолютный центр тяжести системы а).

Соответственно движение каждой материальной точки будет обусловлено совокупностью р+F_упр. Где р - начальный импульс, а F_упр - сила стремящаяся компенсировать разницу скоростей материальных точек.

Однако, нас интересует не поведение каждой отдельной точки системы а следующие обобщения, подтверждающие начальные рассчеты:

Во первых, линейный импульс системы АВ1В2 будет равен импульсу материальной точки соответствующей центру массы - а. Так как на неё не действует центростемительная сила.

Во вторых, F_упр компенсирует разность скоростей отдельных материальных точек относительно общего центра масс а. Соответственно - линейное ускорение любой материальной точки АВ1В2 будет равно поступательному ускорению точки а плюс ускорение вращения.

р_АВ1В2 = р_поста+р_вр

В третьих, если относительно конструкции АВ1В2 а (центр тяжести) располагается ровно посередине, соответственно первоначальный момент силы для а:

М_а = Fd
где d - одна вторая расстояния от осей соединения АВ1 и АВ2.

Соответственно М_а = F/2

В четвертых, если при равноускоренном вращении каждой материальной точке конструкции ей соответствует другая диаметрально расположенная материальная точка, общий импульс вращения системы равен 0.

р_вр = 0

При этом следует учесть, что в отношении материальных точек детали В1 будет действовать совокупность центростремительных сил, которая в каждый момент времени будет равнозначна материальным точкам В2, за минусом собственной центростремительной силы В1.

В пятых. Импульс поступательного ускорения будет соответствовать импульсу вращения - р_пост = р_вр только относительно каждой отдельно взятой материальной точки. Общий же импульс поступательного ускорения АВ1В2 не будет равен импульсу вращения, что следует из вывода четыре.

И шестое. После прекращения взаимодействия АВ2 - В1 центробежные и центростремительные силы АВ1В2 компенсируются и центр вращения постепенно перейдет в точку общего центра масс - а.

Теперь мы можем вернуться к неравенству М_А+М_В2 <> -М_В1

Итак, из вышесказанного мы видим что данное неравенство обусловлено действием центростремительных сил, различным по отношению к АВ1 и В2 во время приложения импульса силы.

При этом, не следует забывать, что приложенная к маховику энергия могла быть как электрической, так и механической (запасенной в сжатой пружине), соответственно являясь потенциальной внутренней энергией системы.

Внутренние потенциальные силы могут изменить импульс замкнутой системы при переходе в кинетическую энергию вращения, если сумма векторов возникших центробежных сил не соответствует общему центру тяжести данной системы.

Но данное определение является скорее лишь следствием иного факта:

Замкнутые системы являются неинерциальными, если в них содержаться активные элементы имеющие ось вращения не соответствующую общему для системы центру тяжести.

Ну а теперь, когда мы разобрались с теорией получения направленного импульса в замкнутой системе, давайте вернемся к системе представленной на рис.2.

Как мы уже знаем, приложенная для вращения маховика сила F в равной степени воздействовала на детали АВ2 и маховик В1. Однако результатом её действия стало не только взаимное вращение АВ2-В1, но и смещение общего центра тяжести относительно независимой точки координат.

При этом, обсуждая движение системы АВ1В2, мы убедились, что некоторые законы механики общепринятые для замкнутых систем не отражают происходящие в данной системе процессы. Однако, для этой системы, как и для всех остальных свойственен закон сохранения энергии.

Рассмотрев процесс первоначального ускорения системы АВ1В2 через призму данного закона, мы получим следующий результат:

Е_к - кинетическая энергия для АВ2 и В1 в момент приложения силы F распределилась поровну согласно третьему закону Ньютона, однако, возникшая при этом центростремительная сила в замкнутой системе АВ1В2 передала часть Е_к АВ2 - В1.

Поэтому, мы должны учитывать, что суммарное воздействие сил на В1 изменило параметры каждой материальной точки таким образом что мы можем рассматривать перемещение (и соответственно кинетическую энергию Е_АВ1В2) АВ1В2 отдельно от перемещения и Е_к В1, как производную от воздействия разнонаправленных сил.

Соответственно мы получим равенство - Е_АВ1В2 = Е_В1,

При этом, из вышеперечисленных расчетов, мы помним что совокупная кинетическая энергия каждой материальной точки конструкции АВ1В2 распределялась поровну между поступательным вектором движения и вращением.

Соответственно - Е_АВ1В2 = Е_пост + Е_вр, где Е_пост = Е_вр

Значит общий вид распределения кинетической энергии в конструкции АВ1В2 будет выглядеть следующим образом - Е_{пост АВ1В2} + Е_{вр АВ1В2} = Е_В1

При этом, интересующий нас вектор поступательного движения составит 25% от первоначально приложенной силы.

Именно поступательный вектор нас и интересует, а не вращение системы. Поэтому не дожидаясь когда центробежные силы развернут конструкцию АВ1В2, прервём действие силы между АВ2 и маховиком В1.

Теперь накопленная в маховике кинетическая энергия сохраняется, но благодаря отсутствию у маховика направленного вектора силы, она может рассматриваться как потенциальная энергия системы, не влияющая на направление движения. Строго говоря, потенциальной по определению она не является, оставаясь кинетической, но, учитывая отсутствие её влияния на перемещение АВ1В2 на определённом отрезке времени, введем такое понятие как - нейтральная кинетическая энергия - Е_н. Согласно закону сохранения энергии Е_н = Е_к.

Определение: нейтральной кинетической энергией системы Е_к является такое состояние кинетической энергии, действие которой не оказывает влияние на систему в данном промежутке времени.

Как мы видим, приведенные выше процессы не противоречат закону сохранения энергии.

Фактически, речь идет о частном случае перехода части энергии из кинетической в нейтральную (относительно потенциальную).

Именно данное решение лежит в основе создания безопорных систем разнообразных конструкций:

В замкнутой системе возможно такое состояние кинетической энергии, которая не оказывает воздействие на систему в данный промежуток времени, и может перемешаться относительно исходной точки в системе координат не изменяя параметров системы.

Однако, рассмотрим действие данной системы во второй фазе движения.

Применим равный первоначальному, но обратный по направлению импульс силы F для В2 - АВ1. Теперь момент силы М для АВ1 будет положительным, а для В2 отрицательным.

При этом необходимо учесть, что в системе АВ1 маховик В1 имеет нейтральную кинетическую энергию, то есть действие этой энергии не распространяется на взаимодействие АВ1 - В2.

Соответственно мы получим момент силы направленный по ходу движения системы, но со знаком минус. Что это даст, прекрасно видно на рисунке 2.

Теперь вращающийся маховик В2 будет останавливать вращение системы. Но как мы знаем из предыдущих расчетов, действие импульсов сил для каждой материальной точки АВ1В2 является совокупностью векторов поступательного движения и центростремительных сил обуславливающих вращение системы. В данном случае вторая фаза ускорения удвоит импульс поступательного движения, и аннулирует первоначальное вращение.

- Е_В1 = Е_{пост АВ1В2} + Е_{вр АВ1В2}
Е_{пост АВ1В2}-(Е_{вр АВ1В2}) = Е_В2

Где отрицательные значения обусловлены формулой момента силы М= +-F, для вращения "по" и "против" часовой стрелки.

Сложив результаты обоих фаз ускорения, мы получим следующий результат:

- Е_В1 = Е_{пост АВ1В2} + Е_{вр АВ1В2} + Е_{пост АВ1В2} - Е_{вр АВ1В2} - Е_В2
Е_В1 + 2 Е_{пост АВ1В2} - (Е_В2) = 2 Е_{пост АВ1В2}

Из данного выражения мы видим, что вращающиеся в противоположном направлении маховики В1 и В2 могут при их одновременном использовании аннулировать накопленную в них кинетическую энергию. Однако, есть более интересный вариант её использования.

Как мы уже выяснили раньше, запасенная в маховиках кинетическая энергия не имеет направленного вектора силы. Следовательно, ничто не может нам помешать развернуть маховики на 180 градусов относительно оси первоначального движения!

Соответственно, проделав эту операцию, мы сможем использовать накопленную в них энергию для третьей и четвертой фазы ускорения.

Итак, вполне простое и очевидное решение найдено. Маховик, как точка опоры, никуда не улетает, от него вполне можно оттолкнуться использовав сектор смещения для вращательно-поступательного движения, и тут же развернуть маховик для повторного использования энергии.

Из всего вышесказанного мы можем сделать вывод:

Безопорное движение возможно при взаимодействии между двумя (или несколькими) вращающимися объектами, если сумма приложенных векторов сил не соответствует центру тяжести данной системы, и (или) сумма векторов торможения не соответствует системе координат ускорения.

Проще говоря, разнообразных систем безопорных двигателей может быть довольно много. Это и парные "качели" описанные в данном тексте, и единичные круговые элементы. Неплохо выглядит вариант с использованием нескольких двигателей вращающихся по кольцу вокруг корабля.

P.S.

Все придуманные за девятнадцать лет варианты перечислять нет смысла. Пожалуй, стоит лишь пожалеть о тех годах, что данный проект пролежал без движения. Причина столь долгого срока банальна - за все эти годы я так и не смог достучаться ни до одной организации способной использовать мою идею. Теперь я посылаю её в Интернет, понимая, что для патентования она потеряна.

Однако, это далеко не единственная имеющаяся у меня интересная идея. Я разработал схему прибора способного заменить компьютерную "мышь" при этом освобождая вторую руку. И это не прототип джойстика или педали. К тому же себестоимость серийного производства данного устройства едва ли дороже оптической мыши. Я знаю, как можно достаточно просто создать программу для введения пароля, которую не взломает ни один "взломщик" использующий систему подбора.

Есть даже оригинальная идея создания термоядерного реактора на горячей плазме, которая, возможно, решит проблему не решенную в "Токамаках". По крайней мере, то, что я смог выяснить из соответствующей литературы лишь подтверждает правильность возможного решения.

Идей много - а вот возможности реализации нет. Я, увы, живу в Магадане, где не смог даже найти специалиста хорошо знающего патентное право.

Надеюсь, эта статья привлечет внимание к моей скромной персоне тех, кто способен претворить мои идеи в жизнь. Будет обидно если они так и пропадут, не увидев свет. Жду предложений о сотрудничестве.